What Is Measured By The Denominator Of The Z-Score Test Statistic? A z-score is a measure of how many standard deviations a data point is away from the mean. The denominator of the z-score formula is the standard deviation of the population.
This means that the denominator measures the spread of the data.
A larger denominator indicates that the data is more spread out, while a smaller denominator indicates that the data is more clustered around the mean.
Definition of the Denominator in the Z-Score Test Statistic: What Is Measured By The Denominator Of The Z-Score Test Statistic?

The denominator of the z-score test statistic represents the standard deviation of the population from which the sample is drawn. It provides a measure of the spread or variability of the data in the population.
The z-score formula is calculated as follows:
“`z = (x
μ) / σ
“`
The denominator of the z-score test statistic measures the standard deviation of the population from which the sample was drawn. Understanding this concept is crucial in various fields, including occupational health and safety. Under The Occupational Health And Safety Act Employees Must ensure a safe working environment by adhering to regulations that often involve statistical analysis.
Therefore, comprehending the denominator of the z-score test statistic is essential for interpreting data and making informed decisions in both research and practical settings.
where:
- z is the z-score
- x is the sample mean
- μ is the population mean
- σ is the population standard deviation
The denominator, σ, serves as a reference point against which the deviation of the sample mean (x – μ) is measured. A larger standard deviation indicates greater variability in the population, resulting in a smaller z-score for a given deviation from the mean.
Conversely, a smaller standard deviation leads to a larger z-score.
Example
Consider a sample of 100 observations with a mean of 50 and a standard deviation of 10. If the population mean is known to be 45, the z-score for this sample would be:
“`z = (50
45) / 10 = 0.5
“`
The z-score of 0.5 indicates that the sample mean is half a standard deviation above the population mean.
Components of the Denominator
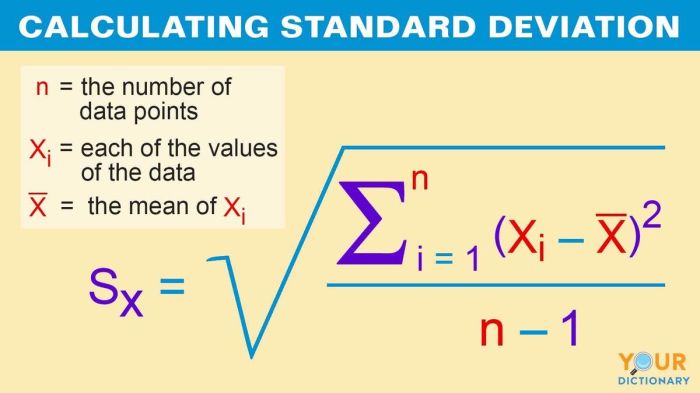
The denominator of the Z-score test statistic is composed of two key elements: the standard deviation and the sample size. Both components play crucial roles in determining the statistical significance of the test statistic.
Standard Deviation
The standard deviation is a measure of the dispersion or spread of data around the mean. A smaller standard deviation indicates that the data is clustered closely around the mean, while a larger standard deviation suggests a wider distribution. In the Z-score formula, the standard deviation serves as the denominator, allowing us to standardize the distribution and compare data points from different populations.
Sample Size
The sample size refers to the number of observations in a given data set. It is an important factor in the Z-score test statistic because it affects the precision of the estimate. A larger sample size typically leads to a more precise estimate of the population mean and, consequently, a more powerful test statistic.
Calculation of the Denominator
Calculating the denominator of the z-score test statistic involves a straightforward process that considers the sample standard deviation and the sample size. Here’s an overview of the steps and the formula used:
The denominator is calculated as the square root of the sample size divided by the sample standard deviation. This formula is represented as:
$$\sigma = \sqrt\fracns^2$$
The denominator of the z-score test statistic measures the standard deviation of the sampling distribution. It represents the variability of the sample mean across all possible samples of the same size drawn from the population. This concept can be illustrated with Coffee Memes Funny , which humorously capture the diverse experiences and emotions associated with coffee consumption.
Just as the denominator of the z-score reflects the variability of sample means, these memes highlight the range of reactions to coffee, from the invigorating to the comical.
Steps Involved in Calculating the Denominator
- Calculate the sample standard deviation (s):Determine the standard deviation of the sample data using an appropriate statistical formula or software.
- Obtain the sample size (n):Determine the total number of observations in the sample.
- Apply the formula:Substitute the values of s and n into the formula above to calculate the denominator.
Interpretation of the Denominator
The denominator of the z-score test statistic, denoted by σ or s, plays a crucial role in determining the value of the z-score. It affects the z-score in two primary ways:
1. Magnitude: The denominator influences the magnitude of the z-score. A larger denominator (i.e., a larger standard deviation) results in a smaller z-score, while a smaller denominator (i.e., a smaller standard deviation) leads to a larger z-score. This is because the standard deviation is used to normalize the difference between the sample mean and the hypothesized mean.
2. Sign: The denominator also affects the sign of the z-score. A positive denominator indicates that the sample mean is greater than the hypothesized mean, while a negative denominator indicates that the sample mean is less than the hypothesized mean.
This is because the standard deviation is always positive, and the sign of the difference between the sample mean and the hypothesized mean is preserved in the z-score.
Implications of a Large or Small Denominator, What Is Measured By The Denominator Of The Z-Score Test Statistic?
The size of the denominator has important implications for the interpretation of the z-score:
- Large Denominator:A large denominator indicates a greater spread or variability in the data. This means that the sample mean is less likely to be significantly different from the hypothesized mean, resulting in a smaller z-score and a lower probability of rejecting the null hypothesis.
- Small Denominator:A small denominator indicates a smaller spread or variability in the data. This means that the sample mean is more likely to be significantly different from the hypothesized mean, resulting in a larger z-score and a higher probability of rejecting the null hypothesis.
Applications of the Denominator

The denominator of the Z-score test statistic is a versatile tool that finds applications in a wide range of statistical analyses. It serves as a key component in various statistical methods and helps researchers understand and interpret data effectively.
In Hypothesis Testing
In hypothesis testing, the denominator plays a crucial role in determining the significance of the observed difference between a sample and a hypothesized population value. By providing a measure of the standard deviation of the sample, the denominator allows researchers to calculate the probability of obtaining the observed difference if the null hypothesis is true.
This information is essential for making inferences about the population and drawing meaningful conclusions.
In Confidence Intervals
The denominator is also used in constructing confidence intervals, which provide a range of plausible values for an unknown population parameter. By incorporating the standard deviation of the sample, the denominator helps determine the width of the confidence interval and the level of confidence associated with the estimate.
This information enables researchers to make informed decisions about the reliability of their findings.
In Power Analysis
In power analysis, the denominator is used to calculate the power of a statistical test, which represents the probability of correctly rejecting the null hypothesis when it is false. By understanding the denominator’s role in power analysis, researchers can design studies with sufficient sample sizes to achieve the desired level of sensitivity and minimize the risk of Type II errors.
In Meta-Analysis
Meta-analysis, a statistical technique that combines the results of multiple studies, also utilizes the denominator. The denominator helps calculate the pooled standard deviation, which is used to estimate the overall effect size and determine the significance of the combined results.
This information enables researchers to draw more robust conclusions based on the cumulative evidence from multiple studies.
Conclusive Thoughts
The denominator of the z-score test statistic is an important part of the formula. It measures the spread of the data and affects the z-score value. A larger denominator indicates that the data is more spread out, while a smaller denominator indicates that the data is more clustered around the mean.
Answers to Common Questions
What is the denominator of a z-score?
The denominator of a z-score is the standard deviation of the population.
What does the denominator of a z-score measure?
The denominator of a z-score measures the spread of the data.
How does the denominator of a z-score affect the z-score value?
A larger denominator indicates that the data is more spread out, while a smaller denominator indicates that the data is more clustered around the mean.