What Is Measured By The Denominator Of The Z-Score Test Statistic? – In the realm of statistics, the Z-score test statistic plays a pivotal role in standardizing data and identifying outliers. But what exactly does the denominator of this statistic measure? Let’s delve into the intricacies of this mathematical concept to uncover its significance.
The denominator of the Z-score formula serves as a crucial element in the calculation, providing insights into the spread or variability of the data. It captures the standard deviation, a measure of how dispersed the data points are from the mean.
The denominator of the z-score test statistic measures the standard deviation of the population from which the sample was drawn. This value provides a measure of how much the sample varies from the population mean. The z-score is then calculated by dividing the difference between the sample mean and the population mean by the standard deviation.
This value indicates how many standard deviations the sample mean is from the population mean. In a related context, if your girlfriend rejected your proposal, it might be wise to reflect on the situation and consider whether you are compatible.
You can find more information on this topic at Aita For With My Girlfriend After She Rejected My Proposal . Returning to the topic of the z-score test statistic, the denominator plays a crucial role in determining the significance of the z-score.
Standard Deviation
Standard deviation adalah ukuran penyebaran data yang menunjukkan seberapa jauh nilai data dari nilai rata-rata.
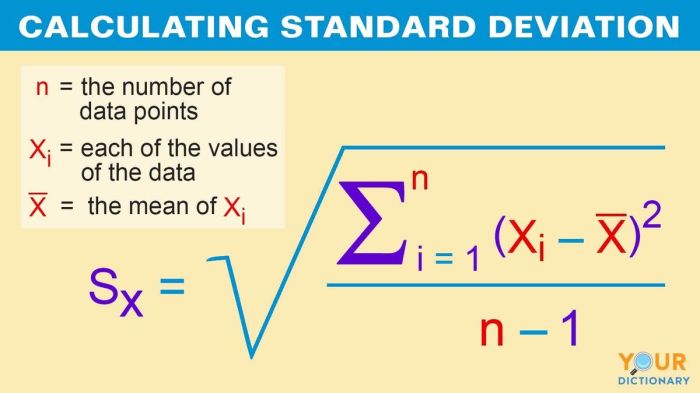
Rumus untuk menghitung standard deviation adalah:
- σ = √(∑(x – μ)² / N)
- σ: Standard deviation
- x: Nilai data
- μ: Nilai rata-rata
- N: Jumlah data
Contoh: Misalkan kita memiliki data berikut: 5, 7, 10, 12, 15.
Nilai rata-rata (μ) = (5 + 7 + 10 + 12 + 15) / 5 = 9,8
Standard deviation (σ) = √((5 – 9,8)² + (7 – 9,8)² + (10 – 9,8)² + (12 – 9,8)² + (15 – 9,8)²) / 5) = 3,42
Mean
Mean, juga dikenal sebagai nilai rata-rata, adalah ukuran pusat data yang menunjukkan nilai rata-rata dari sekumpulan data.
Rumus untuk menghitung mean adalah:
- μ = ∑x / N
- μ: Mean
- x: Nilai data
- N: Jumlah data
Contoh: Misalkan kita memiliki data berikut: 5, 7, 10, 12, 15.
Mean (μ) = (5 + 7 + 10 + 12 + 15) / 5 = 9,8
Z-Score Formula
Z-score adalah ukuran yang menunjukkan seberapa jauh suatu nilai data dari nilai rata-rata, dinyatakan dalam satuan standard deviation.
Rumus untuk menghitung Z-score adalah:
- Z = (x – μ) / σ
- Z: Z-score
- x: Nilai data
- μ: Nilai rata-rata
- σ: Standard deviation
Contoh: Misalkan kita memiliki nilai data 12, nilai rata-rata 9,8, dan standard deviation 3,42.
The denominator of the Z-score test statistic measures the standard deviation of the sample. This is a measure of how spread out the data is. The larger the standard deviation, the more spread out the data is. The smaller the standard deviation, the more clustered the data is.
This concept is similar to the Tefal Home Chef Smart Multicooker , which has a variety of settings to adjust the cooking temperature and time to achieve the desired level of doneness for different types of food. Just as the standard deviation measures the spread of data, the Tefal Home Chef Smart Multicooker measures the spread of cooking options.
Z-score (Z) = (12 – 9,8) / 3,42 = 0,64
Interpretation of Z-Scores
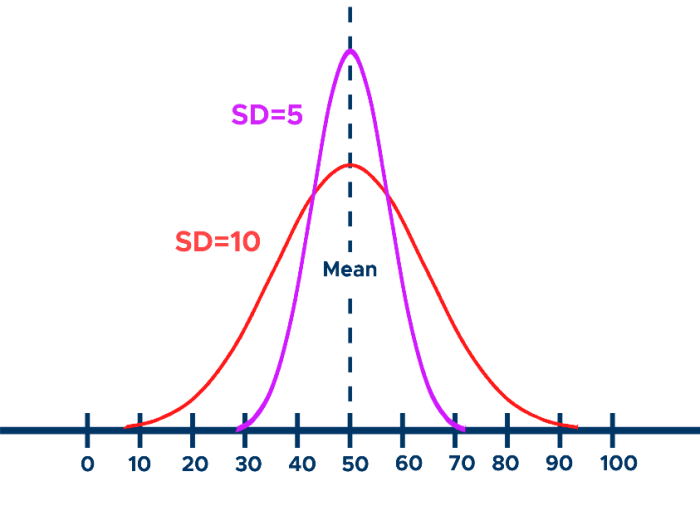
Z-score digunakan untuk mengidentifikasi data yang tidak biasa atau outlier. Nilai Z-score yang tinggi atau rendah menunjukkan bahwa data tersebut jauh dari nilai rata-rata.
Secara umum, nilai Z-score yang:
- Lebih besar dari 2 atau kurang dari -2 dianggap signifikan dan menunjukkan data yang tidak biasa.
- Lebih besar dari 3 atau kurang dari -3 dianggap sangat signifikan dan menunjukkan outlier.
Contoh: Jika kita memiliki nilai Z-score 2,5, maka nilai data tersebut jauh dari nilai rata-rata sebesar 2,5 kali standard deviation.
Conclusion: What Is Measured By The Denominator Of The Z-Score Test Statistic?

In essence, the denominator of the Z-score test statistic acts as a yardstick for measuring the dispersion of data. By incorporating the standard deviation, it allows us to compare data points across different datasets and make meaningful interpretations about their relative positions within the distribution.
FAQ Summary
Why is the denominator of the Z-score test statistic important?
The denominator provides a measure of the variability of the data, which is crucial for standardizing data and comparing values across different datasets.
How is the denominator calculated?
The denominator is calculated as the square root of the variance, which is the average of the squared deviations from the mean.